自分の参加している機械学習勉強会で発表するために読んだ論文のメモ書き。 このサイトを $\TeX{}$ 対応させたのもこの記事を書きたかったがため。

　NeurIPS 2019の採用論文で、多変量時系列データを対象に埋め込み表現を作るという内容。 要は時系列データ相手のWord2Vec。

　論文は こちら。 (NeurIPS版よりもarXiv版の方がAppendixが付いていて、より詳細なのでオススメ)著者が公開しているコードは GitHub で公開されている。

Abstract

　時系列の普遍的な埋め込み表現を学習する教師なし法の提案。Causal Dilated Convolutionを使ったエンコーダと時間ベースのネガティブサンプリングを使用するTriplet Lossを組み合わせて可変長・多変量時系列の汎用表現を取得することができる。

利点 … 長さに関してスケーラブル。

Intro

　NLPや画像分野ではたくさんの表現学習についての研究が行われているが、時系列用の汎用的な表現学習についての研究は少ない。

なぜか

  1. 時系列データにラベル付けされている事がほとんどないか、あってもまばら。
  2. 時系列データの長さが同じでなくても同じ表現を返す必要がある。
  3. 学習時間と推論時間の両方でスケーラビリティと効率性が重要であり、実際に遭遇する短い時系列と長い時系列の両方に対応しなければならない

　評価実験は UCR/UEA 時系列データベースにあるデータセットを使って評価した。(CNNベースのエンコーダを用いて時系列の汎用表現を計算して、SVMで分類する)

訓練

　最終的な目的としては、似たような時系列データが入力された時、似た様な表現を出力される様にしたい。しかもそれを教師なしで。 まず、Triplet Lossを使えば、前者(似た様な系列が来たら似た様な表現を返す)を達成するが可能になるが、元々教師ある学習用の関数なので、後者を解決する。

Triplet Lossとは

$$ \mathcal{L}(A, P, N) = \max\Bigl( ||f(A) - f(P)||^2 - ||f(A) - f(N)||^2 + \alpha, 0\Bigr) $$

　ここで、$A$ はアンカー入力、$P$は$A$と同じクラスで、ポジティブ入力と呼び、$N$はネガティブ入力と呼ばれ、$A$とは異なるクラス。$\alpha$はポシティブとネガティブのペアの間のマージン。$f$は埋め込み。
　このLossが0になれば、同じクラス同士の表現は違い表現を、違うクラス同士の表現は全く違う表現を出力できるネットワークが完成する。

　この論文のTriplet lossはword2vecを参考にしている。Word2Vecの一種にCBOWモデルというものがある。CBOWモデルで使われる手法にNegative Sampling というのがある。

「you say goodbye」という文があったとして、sayをターゲット、周りのyou と goodbyeをコンテキストと呼ぶことにして、「you ???? goodbye」で???にsayがくる確率を最大にすることを考える。この時、正例(say)をターゲットにした場合の損失と一緒にn個の負例(say以外の単語)が来たときの損失も一緒に算出し足し合わせ最終的な損失とする

　この仕組みを時系列にも取り入れたい。

　ここで、Fig 1のイラストの様に、入力系列$\bm{y}_i$のランダムな部分系列$\bm{x}^{ref}$を考える。$\bm{x}^{ref}$の表現は、自身の部分系列$\bm{x}^{pos}$に近い物にならなければならない(Positiveな例)。一方で、ランダムに選択された別の時系列$\bm{x}^{neg}$を考える。これは、時系列が十分に長く且つ定常でないなら同じ時系列から採ってもいいし、複数の時系列が利用可能ならランダムに選択して$\bm{y}_j$部分時系列に切り取る。

　word2vecの考え方(というかnegative samplingの考え方)にのっとると、$\bm{x}^{pos}$はword(もしくはターゲット)、$\bm{x}^{ref}$はコンテキスト、$\bm{x}^{neg}$はランダムワード(負例)となる。

　これの損失関数は、

$$ Loss = -\log\Bigl(\sigma\bigl(f(\bm{x}^{ref}, \bm{\theta}) ^\mathrm{T} f(\bm{x}^{pos}, \bm{\theta})\bigr)\Bigr) - \sum^K_{k=1}\log\Bigl(\sigma\bigl(-f(\bm{x}^{ref}, \bm{\theta}) ^\mathrm{T}f(\bm{x}_k^{neg}, \bm{\theta})\bigr)\Bigl) $$

　ここで$\sigma$はsigmoid関数。 $f(\cdot)$ はパラメータ $\bm{\theta}$ を持つニューラルネット

例えば、

$$ \bm{x}^{ref} = \begin{bmatrix} 3.0 \\ 2.0 \end{bmatrix}, \bm{x}^{pos} = \begin{bmatrix} 2.5 \\ 1.8 \end{bmatrix}, \bm{x}^{neg} = \begin{bmatrix} -3.0 \\ -2.0 \end{bmatrix} $$

の様な埋め込む表現が出来たとしよう。

　上の式にこれを代入すると、

$$ -\log(\sigma(11.1)) - \log(\sigma(-13.0)) \fallingdotseq 0.0 $$

となるわけだ。つまり、この関数で計算される損失を0になる様にネットワークを訓練すれば、$\bm{x}^{ref}$ と $\bm{x}^{pos}$ は近い表現に、$\bm{x}^{ref}$ と $\bm{x}^{neg}$ は明らかに遠い表現を生成できる様になるわけだ。よく出来ている。

　訓練の手順は、以下のAlgorithm 1を用いてランダムに選択したタプル$(\bm{x}^{ref}, \bm{x}^{pos}, (\bm{x}_{k}^{neg})_k)$を用意、 任意のエンコーダを用いて各ペアに対応する表現を生成、上記の式を用いて算出した損失を最小にする。

　全体の計算とメモリの計算量は$\mathcal{O}(K \cdot c(\mathcal{f}))$ であり、ここで、$c(\mathcal{f})$ は$\mathcal{f}$を評価して、逆伝播するコストである。

Encoder Architecture

  1. 時系列から関連する情報を抽出する必要がある。
  2. 訓練とテストの両方で時間とメモリ効率が良い必要がある
  3. 可変長入力が可能である

の3点を満たす必要がある。

　Exponentially Dilated Causal Convolutionを使う。これは名前の通り、指数関数的に拡張された畳み込みを導入さしており、一般的な畳み込みと比較して、ネットワークの受容野を指数関数的に増加させることにより、一定の深さでの長距離依存性をより良く捕捉することができる為、1つ目の問題は解決。2つ目はRNNに比べ、並列化が可能なCNNなので、これも解決。

　可変長に対応するってのは、ネットワーク内でtorch.nn.AdaptiveMaxPool1d(1) いわゆるGlobal MaxPoolingを使っているので(ちょっと強引に)可変長対応している。

Causal ConvolutionとDilated

　Conv層はカーネル(フィルタ)というものを使って畳み込み処理を行う。このカーネルとの積をとる相手をn個飛ばしにしたのがDilated Convolution。

下の図は、dilated=2 の畳み込み。ちなみに、dilated=1 は通常の畳み込みと同じ。

大抵のライブラリなら畳み込み層のインスタンス生成時に引数で設定すればよくて、PyTorchならtorch.nn.Conv1d(..., dilation=...)で試すことができる。

これの利点は、少ないパラメータでより広い範囲の情報を参照することが出来る点。



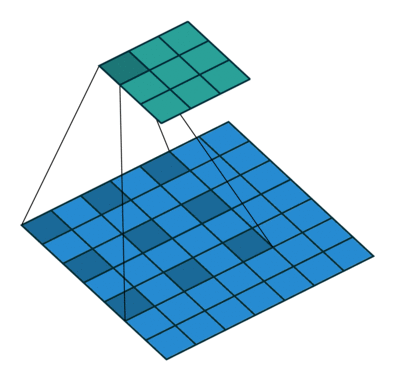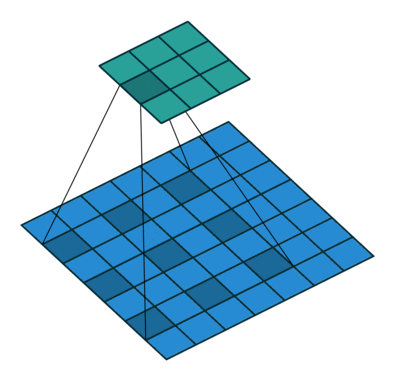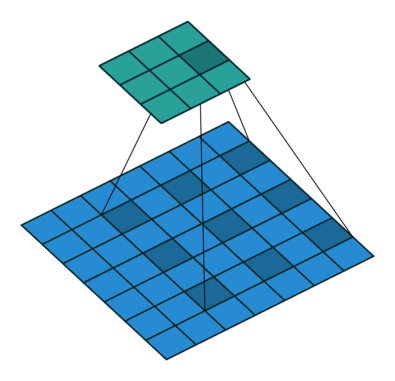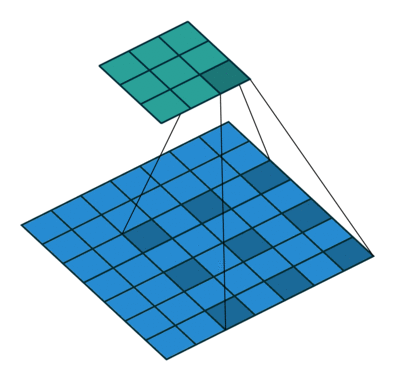
カーネルサイズ3のconvを適用した場合、



赤点の周囲1ピクセルを参照する処理になっているが、dilation=2の場合、





　赤点の周囲一つ飛ばしで参照することになるので、参照範囲だけで言えば、kernel size = 5と同じになる。つまり、計算量やパラメータの数を抑えつつ、広い範囲を参照することのできる仕組みがDilated Convolution。

　次にCausal Convolution。 これは一種のマスキングで、上のDilated Convの図を見ると分かりやすいが、Convは未来の情報も使って出力を計算する。 これを回避するための構造。
　実装は、GluonTSの実装を見れば分かりやすい。

　以上の2つを組み合わせたものがDilated Causal Convolution。

Reference: WaveNet - A Generative Model for Raw Audio [arXiv:1609.03499], ご注文は機械学習ですか？



あとは、Weight Norm, Leaky ReLU, Residual構造を組み合わせて次の様なモジュールを作る。




ここで、$i$は$i$番目の層という意味。初期設定では10層。

実験結果

　NVIDIA Titan Xp × 1を使って実験。OptimizerはAdam。先に説明した損失関数を使ってEncoderを訓練する。

　次に、訓練したEncoderを使って生成した特徴表現と対応するラベルを使ってsklearn.svm.SVCを学習させ分類精度を観察する。 SVMは Radial basis function kernelを使っている。分類性能は若干SVMの能力に頼っている可能性があることに注意。

分類

分類タスクを解かせることで以下3点を確認する。

  • 既存の教師なし学習法よりも優れ、且つ最新の教師あり学習法に近い性能を発揮することを示す
  • ラベル付が少ない場合においてDeep系の教師あり学習よりも高い性能を出すことを示す
  • 転移可能な表現を提供できることを示す

まずデータセットを訓練・テストに分割、訓練セットを使って教師なしでエンコーダを訓練。
次にデータセットのラベルと生成した特徴を使ってRBFカーネルを使ったSVMを訓練。
テストセットの分類性能を評価する。

　データセットは、UCR/UEAアーカイブを使った。それぞれは有名なベンチーマークなので興味があれば確認してほしい。

　分類精度の表は論文の付録を参考にしてほしい。ここでは、一部を示す。



　また、生成した特徴表現をt-SNEを使って可視化するとこんな感じになるそう。 分離可能かどうかは完全にデータセットに依存するようだ。


時系列の教師なし表現学習面白い。